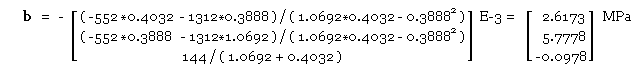
EXAMPLE
The joint of the previous problem is made with an E41xx electrode to AS 1250 in which the minimum safety factor is laid down as √3. What size of fillet should be used ?
Recognising the essential asymmetry of the run, analysis will be based on the unified technique.
Run Geometry
Employing the same axes as used previously, the properties are unchanged. However it should be noted that Ixy, though calculated, was not previously employed. This is now rectified.
Centroidal Loading
The force of [ -4 3 12 ]' kN is applied at the point [ -24 54 400 ]' mm from the centroid. Transferring this force to the centroid gives rise to the centroidal moment of :
M = r x F = [ -24 54 400 ]' x [ -4 3 12 ]' = [ -552 -1312 144 ]' kN.mm
b-Vector
Using ( 4a) for this planar case :-
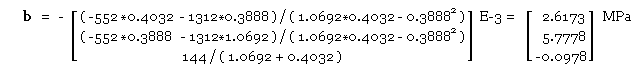
|
Line A-B Search
From ( 5a) the t-matrix may be evaluated since :-
sin θ = ( yB - yA ) / LAB = 1 ; cos θ = ( xB - xA ) / LAB = 0
| Point A : | r | = | [ -24 -126 0 ]' mm - so from ( 2) |
| q | = | [ 2.6173 5.7778 -0.0978 ]' x [ -24 -126 0 ]' - [ -4 3 12 ]' E3/300 | |
| = | [ 1.0 -7.7 -231.1 ]' N/mm ; resolving via ( 5) with ( 5a) | ||
| q | = | 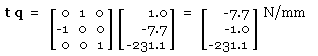
| |
| qe | = | 231.8 N/mm from ( 1) | |
| Point B : | r | = | [ -24 54 0 ]' mm |
| q | = | [ 18.6 -7.7 240.0 ]' N/mm ; so, as above for point A : | |
| = | t q = [ -7.7 -18.6 240.0 ]' N/mm | ||
| qe | = | 231.5 N/mm |
Line B-C Search
Using the same relations as for line A-B above : sin θ = 0 ; cos θ = 1
| Point B : | q | = | [ 18.6 -7.7 240.0 ]' . . . exactly the same as for point B on A-B |
| = | t q = [ 18.6 -7.7 240.0 ]' N/mm | ||
| qe | = | 237.3 N/mm | |
| Point C : | in a similar manner | ||
| qe | = | 463.9 N/mm | |
The program Fillet Welds employs the unified approach - a dialogue with the program for this example illustrates how the unified approach can obviate traditional difficulties with vector recomposition.