Traditional analysis
The traditional approach is limited to planar joint runs, and is commonly restricted to runs having straight segments. It is stated here without proof as it is a particularisation of the unified approach which is derived from first principles below.
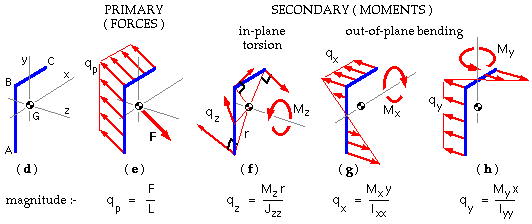
A typical planar joint run comprising two straight segments AB and BC is shown at ( d) below. A convenient Cartesian system is erected at the run's centroid with the run lying in the x-y weld plane. In the sketch, the external loads on the loaded member have been transferred to the run centroid to constitute the known load F, M on the joint - it is this load which is equilibrated by the force intensity q along the run.
The traditional approach treats force intensity along a weld run analogously to stresses in a beam, resolving q into :
- The primary intensity qp is uniform along the run and equilibrates the centroidal force component of the load : qp = - F/L where L is the total length of the run. Thus the sense of qp is opposite to that of F as indicated in ( e).
It is often more straightforward to resolve F and qp into their components qpx = Fx /L and so on.
Primary intensity is analogous to the direct stress in a beam's cross-section which also is uniform - eg. σd = F/A.
- The secondary intensity varies linearly along the run and equilibrates the moment load M. The secondary intensity is split into two components which are each analogous to a basic load building block :
- The in-plane or torsional component of secondary intensity, qz of Fig ( f), equilibrates the moment which is orthogonal to the weld plane, Mz. This moment is analogous to the torque T in a shaft or beam, so Mz is often referred to as the "torque" on the joint.
At any point on the run the torsional intensity, like torsional shear stress in a shaft cross-section :
- lies in the weld plane,
- is directed perpendicularly to the radius r from the centroid to the point in question, and in a sense opposing Mz, and
- is of magnitude given by qz = Mz r/Jzz, ie. the torque load building block with appropriate units (N/mm).
- The out-of-plane or bending component of secondary intensity equilibrates the moment lying in the weld plane - in the general case this latter consists of two Cartesian components, eg. Mx and My in Figs ( g), ( h) above.
At any point on the run the bending intensity - say qx of ( g) - like normal bending stress in a beam cross-section :
- is orthogonal to the weld plane,
- is directed perpendicularly to the coordinate y from the centroid to the point in question, and in a sense opposing Mx, and
- is of magnitude given by qx = Mx y/Ixx, ie. the bending load building block with appropriate units (N/mm).
The total force intensity q is the vector sum of primary and secondary components. Vector summation senses must be deduced by inspection, which can be rather tedious. The procedure is exemplified below.
This example of analysis by the traditional method illustrates some of its drawbacks and . . . .
. . . . confirms that the traditional approach is suitable only for :
- joint runs which are planar, made up of straight segments, and symmetric;
- loading which is simple, eg. consisting of a single force and moment component, because otherwise vector recomposition like that of the above example can become very tedious.
The unified approach on the other hand is completely general and suited to asymmetric runs. It is a vector treatment which does not distinguish between in- and out -of -plane loading, and which is well suited for computer implementation. However before this is examined it is necessary to complete the foregoing by correlating the resultant intensity at any point along the run with the material strength to evaluate the safety factor at that point. To do this, the stresses in the throat plane must be considered.
Throat stresses and joint safety
The following assumptions are made :-
- failure of joints in practice occurs most commonly in the throat so any safety analysis need consider only the throat
- in spite of the extreme stress concentration at the root geometric singularity, the stresses in the critical throat plane may be considered uniform.
These gross simplifications are justified as they enable designs to be compared to actual weld tests using the same fillet loading characterisation.
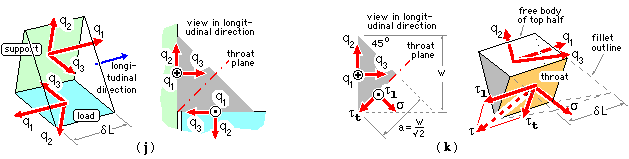
The resultant intensity in global terms q = [ qx qy qz ]' has been evaluated as above for a certain weld element of length δL. The intensity is resolved into components local to the element q = [ q1 q2 q3 ]' in Fig ( j) below - the 1-direction being longitudinal ie. along the run, and the 2- and 3-directions normal to the fillet faces.
For the point C of the preceding example, the 1-2-3 directions local to the joint at C happen to correspond to the global x-y-z senses, so :
qC = [ q1 q2 q3 ]' = [ qx qy qz ]' = [ 18.6 -19.4 -324.5 ]' N/mm
By inspection at the point A on the other hand :
qA = [ q1 q2 q3 ]' = [ qy -qx qz ]' = [ -7.6 -1.0 -27.0 ]' N/mm
The equilibrating components on the loaded member face of the element in ( j) demonstrate that q1 is essentially different to q2 and q3 as these latter appear as shear and normal effects on adjacent fillet faces whereas q1 manifests itself as shear on both faces.
To correlate throat stresses with the known intensity of ( j), we consider equilibrium of a free body of the top half of the fillet, one of whose boundaries is the throat, Fig( k). The uniform stress over the throat consists of a component σ normal to the throat plane, together with two mutually perpendicular shear components lying in the throat plane - the longitudinal shear component τl and the transverse shear component τt.
Since δF = q.δL = σ.δA and the throat width a = w/√2, force equilibrium of the free body ( k) requires :
( ii) τl aδL = q1 δL ;
τt aδL = ( q2 + q3 ) δL/√2 ;
σ aδL = ( q2 - q3 ) δL/√2
Applying the distortion energy failure theory to this plane stress state, the equivalent uniaxial stress in the throat of the fillet element, σe, is given by :-
σe2
= σ2 + 3 τ2
= σ2 + 3 ( τl2 + τt2 ) using Pythagoras
Substituting for the stresses from ( ii) and introducing the concept of the scalar equivalent force intensity qe which causes the same failure tendency as the given q yields :-
( 1) w σe = 2 qe where qe = √( 3/2q12 + q22 + q2 q3 + q32 ) ; σe = S/n
in which S is the strength of the weld material and n is the safety factor at the fillet. Note that ( 1) contains the four indispensible ingredients of a design equation - safety (n), dimensions (the constant fillet size, w), material (characterised by strength S) and loading characterised by the intensity (q).
Like the beam, the final analysis step involves a search along the run to determine the most critically loaded fillet and hence the minimum safety factor of the joint as a whole.
 Copyright 1999-2005 Douglas Wright
Copyright 1999-2005 Douglas Wright
last updated May 2005