
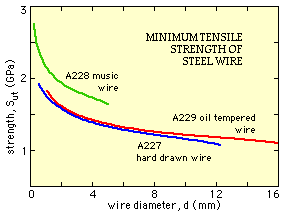
The majority of springs are cold wound from cold drawn carbon steel. The marked increase of tensile strength Sut with decreasing wire diameter d is graphed for three common steel wires - the corresponding expressions in Table 2 below which relate strength to diameter are regressions for data in the Spring Design Manual (op cit) which may be consulted for data on other materials.
| - Sus | ultimate strength in shear |
| - Sys | yield strength in shear - permanent set results if this is exceeded |
| - Ses | fatigue strength in reversed shear corresponding to 10 Mc (107 cycles). |
| TABLE 2 - PROPERTIES OF FERROUS SPRING WIRE | ||||
| material | hard drawn wire | music wire | oil tempered wire | |
| designation | ASTM A227/SAE J113 | ASTM A228/SAE J178 | ASTM A229/SAE J315 | |
| nominal carbon, % | 0.5 - 0.8 | 0.7 - 1.0 | 0.6 - 0.8 | |
| common sizes (d) mm | 0.5 - 12.5 | 0.2 - 5 | 0.8 - 16 | |
| general attributes | cheapest; not for fatigue due to surface defects | best quality; especially for smaller springs | general purpose but fatigue life limited | |
| tensile ult. (Sut) MPa | 2470 +d( 2910 +40d) | 3370 +d( 6560 -230d) | 2630 +d( 2180 +56d) | |
| 1 +d( 2 +0.1d) | 1 +3.5d | 1 +d( 1.6 +0.08d) | ||
| Sus / Sut | 0.52 | 0.50 | 0.63 | |
| Ses / Sut | 0.13 | 0.15 | 0.13 | |
| Sys / Sut | 0.43 | 0.43 | 0.48 | |
Fatigue applications such as engine valves demand a high surface finish of the wire, so the choice of material is based largely on this characteristic which is a result of the method of wire manufacture. Expensive care is taken to maintain the surface of valve spring quality (VSQ) wire free from defects.
Presetting (or "scragging") and shot peening are two manufacturing operations which are carried out after coiling and heat treatment, but before putting a spring into service. They each confer a favourable residual stress distribution in the wire which increases the allowable operating loads.
The stresses in a torsion bar made from an elastic-perfectly plastic material during and after presetting are sketched here. A relatively large presetting load (torque) is applied to cause a band of material under the surface to become plastic while the core of the wire remains elastic ( b).

|
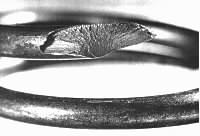
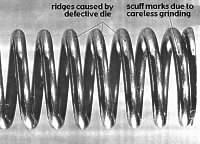
Shot peening involves bombarding the wire with high velocity pellets to impart a surface compression. Residual stresses are more surface- localised than those induced by presetting. Peening is particularly beneficial for fatigue in the presence of surface flaws (die marks, pits and seams), but is appropriate only for wire diameters exceeding 1.5 mm or thereabouts.
Springs destined for arduous duty are invariably preset and/or peened, however in the interests of simplicity we shall not make use of the significantly higher design stresses which these operations allow. The material strengths tabulated above refer to springs without preset or peening.
| 
| 
|
In the absence of such stress raisers, correlation of the repeated loading on a spring with its material's properties in order to ascertain safety is usually carried out via a Goodman analysis. Given the spring material and wire diameter, the shear ultimate Sus and fatigue strength in reversed shear Ses may be found from the literature, or as explained above.
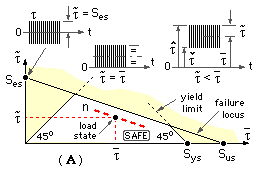 The conservatively straight Goodman failure locus is thus defined in τa - τm space, as shown on the diagram ( A) { nomenclature explanation}.
The conservatively straight Goodman failure locus is thus defined in τa - τm space, as shown on the diagram ( A) { nomenclature explanation}.
Spring loading is almost invariably unidirectional, so τa ≤ τm and loading states occur only to the right of the 45o stress equality line. One such load state is illustrated, lying on a line which corresponds to a safety factor of n, ie. the line joins the points ( Sus/n, 0), (0, Ses/n) and so lies parallel to the failure locus. From similar triangles the Goodman fatigue equation is :
( 4a) τm /Sus + τa /Ses = 1/n in which the stress components are given by
τm = Ks 8 FmC / πd2 where Fm = ( Fhi + Flo ) /2 and
τa = Kh 8 Fa C / πd2 where Fa = ( Fhi - Flo ) /2
The full stress concentration factor Kh is applied to the alternating component τa in ( 4a). Stress redistribution is presumed to follow localised yielding, with the result that stress concentration is usually ignored in figuring the steady component of fatigue loading. The mean stress τm is therefore based on the factor Ks, which accounts only for direct stresses in the torsion equation.
The safe operating window of the Goodman diagram is completed by the yield limit. If ny is the factor of safety against the yield being exceeded, then :
( 4b) τm + τa = Sys/ny since ( τm + τa ) represents the maximum stress.
A fatigue analysis of the preceding example using ( 4a) is carried out in this example.
( 4c) τhi = { 2 Sus Ses / ( Sus + Ses ) } + { ( Sus - Ses ) / ( Sus + Ses ) } τlo where
τhi = Kh 8 C Fhi / πd2 and τlo = Kh 8 C Flo / πd2
Thus for the wire of the foregoing example with stresses in MPa :

The fatigue strength in repeated (one-way) shear S'es forms the basis of a Goodman approach, diagram ( B) which is less conservative than that based on reversed shear, diagram ( A).
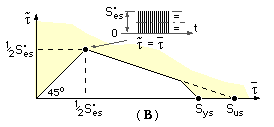 If the test stress varies between zero and S'es, then τa = τm = S'es/2, and the failure line joins the points ( Sus, 0), ( S'es/2, S'es/2 ). The resulting design equation is :
If the test stress varies between zero and S'es, then τa = τm = S'es/2, and the failure line joins the points ( Sus, 0), ( S'es/2, S'es/2 ). The resulting design equation is :
( 4d) τm /Sus + τa ( 2/S'es - 1/Sus ) = 1/n
Since it is rare that the fatigue strength in repeated loading is available, we will henceforth employ ( 4a) and ( 4b) with the fatigue strength corresponding to whatever life is of interest.