τhi = Ks 8 Fhi C / π d2 = Sys /n

Spring design may be based upon charts, computer programs, nomograms or other similar aids - the suitability of any approach depends to a large extent upon the information available :
Whatever approach is used, it is important that the desired spring characteristic is known as fully as possible before starting on detailed calculations. This may necessitate preliminary assumptions, since specification information is often sparse. In a certain fatigue application the maximum operating force may be specified but nothing is stipulated about the minimum, so we might adopt a common rule of thumb which has the minimum force no less that one third of the maximum, to avoid all possibility of spring bounce.
It is usually most expedient to search for a suitable combination of material and wire diameter - together with index C rather than coil diameter D. Wire size must be selected from the available range. The search for suitable index (say 5 ≤ C ≤ 10) is more bounded that a search for mean diameter D. However a space constraint is common - thus the spring may have to fit over a rod, diameter Dr, in which case a space constraint is Di = D - d = ( C -1)d > Dr. Or the spring may have to fit inside a hole of bore Dh, so, realising that a compressed spring may expand diametrically by some 3-4%, the design must satisfy Do = D + d = ( C +1)d < 0.96 Dh.
Selection of the major spring parameters for static applications (say ≤ 104 cycles) in which the maximum load is Fhi, might proceed thus. The material is first selected, and hence the ratio of shear yield strength to tensile ultimate strength ( Sys /Sut ) obtained from Table 2 or similar. The safety factor, n, in this static application may be found from ( 1) :
τhi = Ks 8 Fhi C / π d2 = Sys /n

When this is normalised by the tensile ultimate Sut, the term π/4 d2 Sut emerges, and is recognised as the ultimate tensile load on the wire, Fut. Since Sut is a function solely of the wire diameter (Table 2), then Fut also is dependent only upon diameter, as given in Table 3. The foregoing equation may then be written as :
( 5a) n = Fut /Fe ; Fut = π/4 d2 Sut ; Fe = 2 Fhi C Ks /( Sys /Sut )
Fe is the tensile load on the wire which is equivalent failurewise to the actual maximum load on the spring. While Fut depends on wire diameter for a given material, Fe on the other hand depends only on spring index, C, for a predefined load. Separation of d- and C-effects in this manner greatly assists manual spring design.
In fatigue applications, the Goodman design equation ( 4a) may be manipulated into the same form as ( 5a), however the force Fe is now interpreted as the steady tensile wire load which is equivalent failurewise to the spring fatigue load - components Fm and Fa - and is given by :
( 5b) Fe = 2 Fm C Ks /( Sus / Sut ) + 2 Fa C Kh /( Ses / Sut )
It is noticeable that this fatigue equivalent load, like the equivalent load in the static case, depends only on the spring index for given load and material.
An important consideration in high-speed cyclic applications is the avoidance of surging, where waves of high inter- coil displacement travel along the spring leading to high operating stresses, clashing and impact. Surging arises from resonance between the operating and natural frequencies of the spring, whose mass distribution is significant at the accelerations involved. The spring's fundamental natural frequency, fn, is given by :
( 6) fn = ( d/π na D2 ) √ ( G/8ρ) and, for steel with density ρ = 76.5 kN/m3 this becomes
= 358 / na CD kHz where D is in mm.
To avoid surging, this fundamental frequency must be higher than the operating frequency's highest significant harmonic - usually taken to be the 12th harmonic, though this will depend upon the shape of the load cycle.
Study of the map contours reveals general trends of geometric parameter combinations necessary to meet a specific duty - knowledge of these trends is useful in manual spring design. Clearly the loci of constant coil mean diameters are hyperbolae ( Cd = D). For a certain wire diameter, decreasing the index leads to increased fatigue safety, markedly increased necessary turns, and increased length with a consequent increased tendency to buckle. Buckling propensity is not much affected by wire diameter. Both wire diameter and index have to increase or decrease together to maintain a constant level of safety.
The solution space in the C-d plane is wedge-shaped - figure ( a) below - bounded by fatigue safety ( n = 1) and conditional stability. In practice, this space is constrained further by design factors exceeding unity and by stability which is preferably absolute.
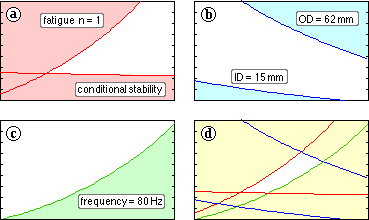 Every dynamic spring is subject to these constraints. Instability, even whilst the spring is guided, can lead to stiffness fluctuations, scuffing, and other undesirables.
Every dynamic spring is subject to these constraints. Instability, even whilst the spring is guided, can lead to stiffness fluctuations, scuffing, and other undesirables.
Contours of spring diametral limits appear in figure ( b) - unlike the general constraints of figure ( a), these diametral limits are relevant only to certain springs. Simultaneous ID and OD limits are unusual.
The requirement for a fundamental natural frequency of at least twelve times the running frequency, results in a bound similar to that of figure ( c) - eg. 12 x 400 cpm = 80 Hz for the sample problem. High speed springs often cannot meet this 'limit', so it should not be regarded as immutable as were the safety / stability limits of figure ( a). Preset and/or peened springs can withstand higher stresses than the untreated springs examined here - for the same duty they would therefore be lighter, possess a higher natural frequency, and would be more suitable for high speed applications.
As a result of all the limits, the above problem's restricted solution space appears as in figure ( d). The form of this space is quite general, though clearly the actual shape in any particular case will depend upon the relative significance of the various bounds. In the above problem for example, the ID limit is over-ridden by the stability bound.
Spring design specifications evidently do not always admit practical solution.