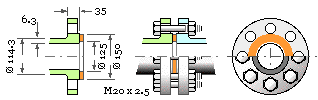
 A Φ 100 mm nominal pipe is equipped with raised face flanges and a spirally wound asbestos filled gasket, 4 mm thick and of the dimensions sketched. It is proposed to use 8 M20 x2.5 class 5.8 bolts for the joint, which is subjected to a fluid design pressure varying between zero and 7.5 MPa.
A Φ 100 mm nominal pipe is equipped with raised face flanges and a spirally wound asbestos filled gasket, 4 mm thick and of the dimensions sketched. It is proposed to use 8 M20 x2.5 class 5.8 bolts for the joint, which is subjected to a fluid design pressure varying between zero and 7.5 MPa.
The whole operation of the joint will need to be checked - leakage tendency as indicated by 'm' and 'y' factors, fatigue of the bolts, and so on.
Dimensions & initial loading
The width of the gasket here is (150-125)/2 = 12.5 mm. AS 1210 table 3.21.6.4(B) states that the effective width, allowing for rotation etc, is 2.52√(width/2) = 6.3 mm.
Gasket OD is 150 mm, so gasket effective ID is 150- 2 x 6.3 = 137.4 mm, and gasket effective area is Ag = π( 1502 -137.42 )/4 = 2844 mm2.
The effective area inside the gasket which is subjected to fluid pressure is Ai = 137.42 π/4 = 14 830 mm2.
Bolts' proof load Fp = 245 x 380 = 93 kN
Assume tightening to 75% proof, then total initial tightening load is Fi = 8 x 0.75 x Fp = 560 kN.
Stiffnesses & joint factor
On the basis of a single bolt and the gasket associated with it . . . .
Gasket stress limitations
Based upon whole gasket . . . .
From Table 3, y = 69 MPa and m= 3.0 for a spiral wound asbestos filled gasket.
The initial gasket stress is Fi/Ag = 560/2844 = 197 MPa > y, so OK.
Check crushing - lacking any recommendations, presume a limiting stress of 2y = 138 MPa ( based on total not effective gasket area ). Based upon this area, the initial ( ie. maximum ) stress on the gasket is 560 x 4/π( 1502-1252 ) = 104 MPa < 2y and so crushing should not be a problem.
Now consider gasket stress when full fluid pressure of 7.5 MPa is applied. From ( 3b) with external fluid load ( or hydrostatic load ) of P = pfluid Ai = 7.5 x 14830 = 111 kN
Fj = Fi - ( 1 -C ) P = 560 -(1-0.59) x 111 = 514 kN { 547 kN }
which corresponds to a gasket stress of pg = Fj /Ag = 514/2844 = 181 MPa { 192 MPa }
Ratio pg /pfluid = 181/7.5 > m = 3.0 so this criterion is satisfied and the gasket should not leak.
Bolt fatigue
Based upon a single bolt . . . .
From Table 2, Su = 0.5 GPa, so Se' = ( 0.55 -0.088 x 0.5 ) x 0.5 = 253 MPa
Assuming rolled threads, Kf = 2.2 ( Table 6 ) and so Se = Se'/Kf = 253/2.2 = 115 MPa
σi = Fi /As = 560/8 x 245 = 286 MPa
σa = CP/2As = 0.59 x 111/2 x 8 x 245 = 17 MPa { 25 MPa }
Applying ( 6a), the safety factor for the load on the bolts themselves ( Fb) is
1/n = σi /Su + σa (1/Su + 1/Se ) = 286/500 +17 x ( 1/500 +1/115) ; n = 1.33 { 1.19 - note effect of small kj }
Alternatively, applying ( 6b) for the safety factor on fluid pressure loading ( P) against bolt fatigue failure
1 = σi /Su + n σa (1/Su + 1/Se ) = 286/500 + n x 17 x ( 1/500 +1/115) ; n = 2.35 { 1.60 }
All-in-all, the joint is satisfactory as it stands. The bolt class is therefore suitable.