EXAMPLE
Repeat the preceding example if the mechanism is imperfect, the imperfection being characterised by an initial out- of- straightness θo when the springs are free.
The analysis is similar to the above except that the free position is defined by θ = θo rather than by θ = 0. So, as the initial deflections must increase :
δ1 = 2b [ ( cosθ + α sinθ ) - ( cosθo + α sinθo ) ] ; |θ| ≥ |θo|
δ2 = 2b [ ( cosθ - α sinθ ) - ( cosθo - α sinθo ) ]
y - yo = 4b ( cosθ - cosθo )
For the system therefore - normalising and differentiating as before :-
U = Σ k δ2/2 + P ( y - yo )
u = U/8kb2 = 1/2 [ ( cosθ - cosθo )2 + α2 ( sinθ - sinθo )2 ] + p ( cosθ - cosθo )
( C) u' = ( cosθo - cosθ ) sinθ + α2 ( sinθ - sinθo ) cosθ - p sinθ
( D) u" = ( cosθo cosθ - cos2θ ) + α2 ( sinθo sinθ + cos2θ ) - p cosθ
The equilibrium path, from ( 1a) and ( C) is evidently :
<
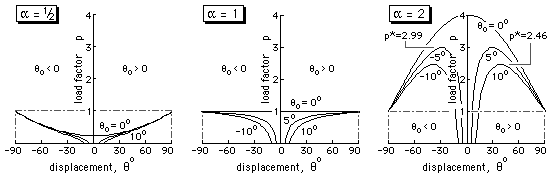
( E) p = cosθo - cosθ + α2 ( 1 - sinθo / sinθ ) cosθ ; |θ| ≥ |θo|
which is plotted below for the same three mechanism proportions as previously, for the perfect case ( θo = 0 ), and for positive and negative imperfections |θo| = 5o and 10o.

|
Thus, for the positive branches, stability is lost if
( F) u" ≤ 0 ie. if sinθ ≥ [ α2 sinθo / ( α2 - 1) ]1/3
and can only occur if α > 1; the corresponding maximum load capacity p* from ( F) being :
p* = cosθo + [ ( α2 - 1 )2/3 - ( α2 sinθo )2/3 ]3/2 ; α > 1
Some values of p* are shown above for α = 2.