Power transmission shafting
Continuous mechanical power is usually transmitted along and between rotating shafts. The transfer between shafts is accomplished by gears, belts, chains or other similar means for matching the torque/speed characteristics of the interconnected shafts - eg. a car needs gears between the engine crankshaft and drive wheel half-shafts. Matching will be examined more closely in later chapters (Squirrel Cage Motors, V-Belt Drives, Spur Gears), here we focus on shafts.
Shafts rotating only at constant speed n (rev/s) are considered here, and as shafts are usually statically determinate they may be examined by the techniques of elementary statics. Also, since
| - | power = force ( N) ∗ linear velocity ( m/s) in translational applications and
|
| - | power = torque ( Nm) ∗ angular velocity ( = 2π n rad/s) in rotational applications,
|
| . . . . then it follows that torque is a major load component in power transmitting rotating shafts.
|
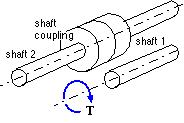
Torque may be transferred to or from the end of one shaft by a second coaxial shaft - this is a pure torque, a twist about the shaft axis. The transfer is accomplished by a shaft coupling (illustrated in the Squirrel Cage Motors chapter) which consists of two often identical half-couplings which are each mounted on one of the shafts before being connected together non-permanently.
The mounting of a half-coupling on a shaft must prevent relative rotation when torque is applied - this is achieved by a positively interlocking element exemplified by a key (or a derivative of this such as a spline) or by friction.
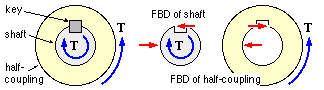 Shown here is the free body of a shaft keyed to a coupling half - the torque on the shaft is equilibrated by an equal and opposite torque on the half-coupling. Free bodies of the individual elements clarify how the key's faces give rise to an equilibrating couple on both the shaft and the half-coupling (refer to the tutorial problems for more details).
Shown here is the free body of a shaft keyed to a coupling half - the torque on the shaft is equilibrated by an equal and opposite torque on the half-coupling. Free bodies of the individual elements clarify how the key's faces give rise to an equilibrating couple on both the shaft and the half-coupling (refer to the tutorial problems for more details).
The typical friction-based mounting below comprises a split tapered bush which is forced by screws into a mating taper
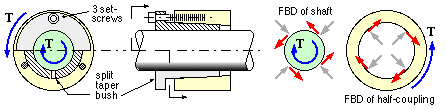 machined in the bore of the half-coupling. The bush contracts onto the shaft causing high pressures and corresponding high surface friction which equilibrates the torque - provided tightening is sufficient.
machined in the bore of the half-coupling. The bush contracts onto the shaft causing high pressures and corresponding high surface friction which equilibrates the torque - provided tightening is sufficient.
Torque may be transferred also at any point along a
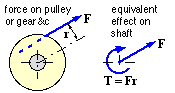 shaft by a gear, belt pulley, or chain sprocket for example, mounted on the shaft as described above. These common elements apply forces offset from the shaft axis, and therefore useful torque T must be accompanied by a corresponding radial load with consequential bending - this is why the generalised shaft design model ( 11) incorporates both torque and bending moment load components.
shaft by a gear, belt pulley, or chain sprocket for example, mounted on the shaft as described above. These common elements apply forces offset from the shaft axis, and therefore useful torque T must be accompanied by a corresponding radial load with consequential bending - this is why the generalised shaft design model ( 11) incorporates both torque and bending moment load components.
A spur gear and a belt pulley are sketched, each subjected to loading tangential to its effective or pitch cylinder of diameter D.
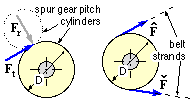 The load on the spur gear arises from inter-tooth contact with its mating gear and comprises two components - the useful tangential component Ft and the unwanted but unavoidable radial component Fr (commonly 0.36 Ft ). Gear forms other than spur ( see the Spur Gears chapter) give rise also to a load component parallel to the shaft axis - but for all gears, shifting the offset force as above, T = Ft D/2.
The load on the spur gear arises from inter-tooth contact with its mating gear and comprises two components - the useful tangential component Ft and the unwanted but unavoidable radial component Fr (commonly 0.36 Ft ). Gear forms other than spur ( see the Spur Gears chapter) give rise also to a load component parallel to the shaft axis - but for all gears, shifting the offset force as above, T = Ft D/2.
A belt, being flexible, cannot withstand compression - the pulley is therefore subjected to two strand tensions Fmax and Fmin both of which must exceed zero. The net torque T = ( Fmax - Fmin ) D/2 is clockwise here. The tension ratio Fmax/Fmin must lie between a lower limit of unity (corresponding to no torque transfer) and an upper limit dictated by incipient belt slip around the pulley. (This may be demonstrated by equally pulling the ends of a bit of rope wrapped around a post, then progressively increasing the pull on one end.) A chain sprocket is similar though the minimum tension may drop to zero due to the positive drive not relying on friction.
The mounting of a half-coupling and the like on a shaft is, locally, intrinsically indeterminate. This is exemplified by the pulley boss illustrated which extends from A to C
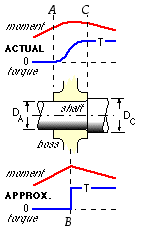 along the stepped shaft. The actual distributions of bending and torque in the shaft are shown. To the left of A and to the right of C there are no immediate transverse loads, so the bending moment is linear. But within AC the boss contributes to the shaft's stiffness and also distributes the pulley load gradually into the shaft, so the bending moment variation is non-linear. Similarly the torque is some constant value (zero here) in the shaft to the left of A and another constant value T to the right of C - within AC the torque increases in a complex indeterminate fashion.
along the stepped shaft. The actual distributions of bending and torque in the shaft are shown. To the left of A and to the right of C there are no immediate transverse loads, so the bending moment is linear. But within AC the boss contributes to the shaft's stiffness and also distributes the pulley load gradually into the shaft, so the bending moment variation is non-linear. Similarly the torque is some constant value (zero here) in the shaft to the left of A and another constant value T to the right of C - within AC the torque increases in a complex indeterminate fashion.
No attempt is made to resolve this bending/torsional indeterminacy - the actual distributions are instead replaced by approximate distributions based on external loads concentrated at the mid-point B. This leads to a bending moment diagram characterised by straight segments and a torque diagram which increases stepwise at B. The approximation is justified in view of unknown stiffness details and stress concentration due to shoulders (used for positive longitudinal location) and mountings (square keys, shrink fits etc.) In this example a cross-section between B and C is critical since the diameter is the smaller DA (neglecting the blending radii which reduce stress concentration at the shoulder), the torque is the fully developed T, and the bending moment is to all intents and purposes the peak MB.
Shafts are supported in two bearings (sliding or rolling) which allow the shafts to turn freely - there is no appreciable torque exerted by the bearings. A sliding bearing needs a lubricant film in the clearance space between shaft and bearing bush;
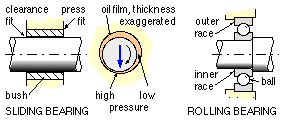 in the fully hydrodynamic bearing illustrated the oil is dragged into the wedge-shaped gap causing a pressure build-up (similar to that in hydroplaning) which supports the shaft without metal-to-metal contact and little friction.
in the fully hydrodynamic bearing illustrated the oil is dragged into the wedge-shaped gap causing a pressure build-up (similar to that in hydroplaning) which supports the shaft without metal-to-metal contact and little friction.
A rolling bearing (of which the ball bearing illustrated is but one example) comprises two hardened races between which a number of identical hardened elements roll. Not shown are various necessary details such as means for preventing axial movement of races, for dust sealing and for lubricant retention.
There are many different embodiments of these two bearing classes. A bearing supports a shaft over a finite axial length and so is intrinsically indeterminate no matter what its form - however it is approximated like the boss ABC above by a concentrated reaction at its mid-point.
The transverse forces on a shaft are seldom coplanar, so it is usually necessary to resolve forces into two convenient orthogonal longitudinal planes and to separately consider bending in each. For example the horizontal shaft ABCD, figure (a), is simply supported in bearings at A, D and carries gears or pulleys at B, C.
The offset gear/belt forces are shifted to the shaft axis as above, giving rise to the shaft bending loads, figure (a). The corresponding torque diagram figure (b) shows that torque is transmitted between B and C
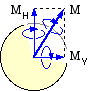 (there is no torque sink outside BC as the bearings can offer no appreciable torsional resistance). The bending loads are resolved into vertical and horizontal planes, figure (c). Treating each plane separately, the bearing reactions are computed and the bending moment diagram completed, resulting in two component BMDs figure (d). Since moments are vectors, the resultant bending moment at any cross-section along the shaft can be found easily from the two components by Pythagoras as M = √( MH2 +MV2 ), recalling that it is the moment magnitude only which is relevant in ( 11).
(there is no torque sink outside BC as the bearings can offer no appreciable torsional resistance). The bending loads are resolved into vertical and horizontal planes, figure (c). Treating each plane separately, the bearing reactions are computed and the bending moment diagram completed, resulting in two component BMDs figure (d). Since moments are vectors, the resultant bending moment at any cross-section along the shaft can be found easily from the two components by Pythagoras as M = √( MH2 +MV2 ), recalling that it is the moment magnitude only which is relevant in ( 11).
Finally, some tips for shaft analysis :-
- Equilibrium in the axial view is usually examined first, to figure out the magnitude of the torque(s) and the locations between which torque is transmitted. Thus the shaft, figure (e) similar to ABCD above, is freely supported in bearings and equipped with
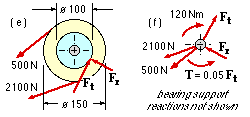
- a 150 mm diameter belt pulley with strand tensions given as 2100 and 500 N
- a spur gear of 100 mm pitch diameter with unknown tangential and radial forces.
Each force is shifted if necessary to pass through the shaft axis whilst introducing the corresponding torque figure (f). Thus starting with the two known belt forces, the net clockwise torque due to their shift is ( 2100 - 500 ) x 0.075 = 120 Nm.
This is the torque T transmitted between belt and gear. The anticlockwise torque introduced when the gear's tangential force is shifted to the axis is Ft x 0.05 Nm, assuming F units are N. For rotational equilibrium therefore 0.05 Ft = 120, ie. Ft = 2400 N. Finally Fr may be taken as 0.36 Ft = 864 N (though note that three sigfigs are unwarranted). All external loads are now known, so they may be resolved into orthogonal planes, figure (c) prior to calculating bending moments.
Note that figure (f) is not a complete free body, however the bearing reactions which are not shown do not contribute to rotational equilibrium.
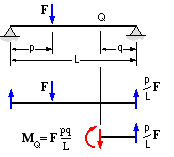
- As shaft loading is concentrated, it is usually easier to calculate bending moments from standard results rather than to prepare a complete bending moment diagram from first principles. Thus a body of length L between simple supports is loaded by a transverse force F located at p from one support. The bending moment at a point Q distant q from the other support is derived in the sketch as
( 12) MQ = F pq/L
- a result which can be applied to superpose the bending effects of multiple loads, though care is needed when load senses differ or loads overhang the supports - it is suggested that the steps shown in the sketch be retraced for these cases.
- Tutorial problem #17 is extremely useful in proving that the maximum equivalent loading Me cannot occur between concentrated loads, so it is necessary to search for the critical cross-section only amongst those cross-sections where (or close to where) loads or supports occur.
This example demonstrates a typical design procedure.
This script applies ( 11) to analyse or synthesise ductile or brittle shafts under static loads.
 Copyright 1999-2005 Douglas Wright
Copyright 1999-2005 Douglas Wright
last updated May 2005
 Shown here is the free body of a shaft keyed to a coupling half - the torque on the shaft is equilibrated by an equal and opposite torque on the half-coupling. Free bodies of the individual elements clarify how the key's faces give rise to an equilibrating couple on both the shaft and the half-coupling (refer to the tutorial problems for more details).
Shown here is the free body of a shaft keyed to a coupling half - the torque on the shaft is equilibrated by an equal and opposite torque on the half-coupling. Free bodies of the individual elements clarify how the key's faces give rise to an equilibrating couple on both the shaft and the half-coupling (refer to the tutorial problems for more details).

 machined in the bore of the half-coupling. The bush contracts onto the shaft causing high pressures and corresponding high surface friction which equilibrates the torque - provided tightening is sufficient.
machined in the bore of the half-coupling. The bush contracts onto the shaft causing high pressures and corresponding high surface friction which equilibrates the torque - provided tightening is sufficient.
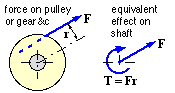 shaft by a gear, belt pulley, or chain sprocket for example, mounted on the shaft as described above. These common elements apply forces offset from the shaft axis, and therefore useful torque T must be accompanied by a corresponding radial load with consequential bending - this is why the generalised shaft design model ( 11) incorporates both torque and bending moment load components.
shaft by a gear, belt pulley, or chain sprocket for example, mounted on the shaft as described above. These common elements apply forces offset from the shaft axis, and therefore useful torque T must be accompanied by a corresponding radial load with consequential bending - this is why the generalised shaft design model ( 11) incorporates both torque and bending moment load components.
 The load on the spur gear arises from inter-tooth contact with its mating gear and comprises two components - the useful tangential component Ft and the unwanted but unavoidable radial component Fr (commonly 0.36 Ft ). Gear forms other than spur ( see the Spur Gears chapter) give rise also to a load component parallel to the shaft axis - but for all gears, shifting the offset force as above, T = Ft D/2.
The load on the spur gear arises from inter-tooth contact with its mating gear and comprises two components - the useful tangential component Ft and the unwanted but unavoidable radial component Fr (commonly 0.36 Ft ). Gear forms other than spur ( see the Spur Gears chapter) give rise also to a load component parallel to the shaft axis - but for all gears, shifting the offset force as above, T = Ft D/2.
 along the stepped shaft. The actual distributions of bending and torque in the shaft are shown. To the left of A and to the right of C there are no immediate transverse loads, so the bending moment is linear. But within AC the boss contributes to the shaft's stiffness and also distributes the pulley load gradually into the shaft, so the bending moment variation is non-linear. Similarly the torque is some constant value (zero here) in the shaft to the left of A and another constant value T to the right of C - within AC the torque increases in a complex indeterminate fashion.
along the stepped shaft. The actual distributions of bending and torque in the shaft are shown. To the left of A and to the right of C there are no immediate transverse loads, so the bending moment is linear. But within AC the boss contributes to the shaft's stiffness and also distributes the pulley load gradually into the shaft, so the bending moment variation is non-linear. Similarly the torque is some constant value (zero here) in the shaft to the left of A and another constant value T to the right of C - within AC the torque increases in a complex indeterminate fashion.
 in the fully hydrodynamic bearing illustrated the oil is dragged into the wedge-shaped gap causing a pressure build-up (similar to that in hydroplaning) which supports the shaft without metal-to-metal contact and little friction.
in the fully hydrodynamic bearing illustrated the oil is dragged into the wedge-shaped gap causing a pressure build-up (similar to that in hydroplaning) which supports the shaft without metal-to-metal contact and little friction.
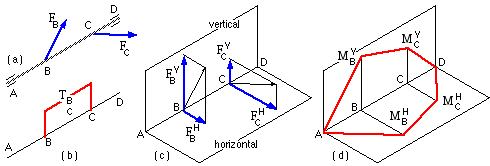
 (there is no torque sink outside BC as the bearings can offer no appreciable torsional resistance). The bending loads are resolved into vertical and horizontal planes, figure (c). Treating each plane separately, the bearing reactions are computed and the bending moment diagram completed, resulting in two component BMDs figure (d). Since moments are vectors, the resultant bending moment at any cross-section along the shaft can be found easily from the two components by Pythagoras as M = √( MH2 +MV2 ), recalling that it is the moment magnitude only which is relevant in ( 11).
(there is no torque sink outside BC as the bearings can offer no appreciable torsional resistance). The bending loads are resolved into vertical and horizontal planes, figure (c). Treating each plane separately, the bearing reactions are computed and the bending moment diagram completed, resulting in two component BMDs figure (d). Since moments are vectors, the resultant bending moment at any cross-section along the shaft can be found easily from the two components by Pythagoras as M = √( MH2 +MV2 ), recalling that it is the moment magnitude only which is relevant in ( 11).

