EXAMPLE
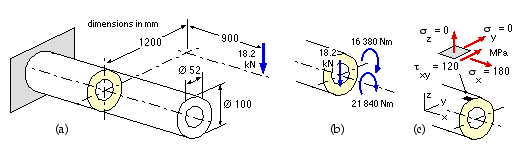
The cantilevered shaft of fig (a) is loaded only by the 18.2 kN force. Ascertain the factor of safety at the hatched cross-section if the shaft is
- ductile with a yield of 350 MPa, or
- brittle with tensile and compressive ultimates of 300 and 750 MPa.
Find all loads on member, resolving any static indeterminacies if necessary
- The 18.2kN force is the sole load here.
Identify load building blocks and potentially critical element(s); evaluate corresponding stress components
- Constructing a free body embracing the load(s) and the required cross-section, the load building blocks are found here to include bending, torsion and direct shear - fig (b). The cross-sectional element of fig (c) is identified as the most critically loaded; the stress components on it are :
- bending : σx = My/I = 16380 x 50 x 64 / π (1004 -524) = 180 MPa
- torsion : τxy = Tr/J = 21840 x 50 x 32 / π (1004 -524) = 120 MPa
The direct shear stress maximises in the centroidal x-y plane at 4V/3A = 4 x 18.2 E3 x 4 / 3 x π (1002 -522) = 4 MPa
 but vanishes at the element in question; its neglect is justified. Other stresses on the element are zero.
but vanishes at the element in question; its neglect is justified. Other stresses on the element are zero.
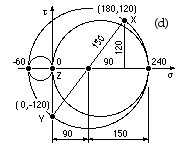
Resolve stresses to ascertain the three principals
Stresses on the x-y faces of the element are resolved by Mohr's circle fig (d) to give the principals in the x-y plane. Since there are no z-stresses, the three principals are 240, 0, -60 MPa.
Apply the relevant failure theory
Ductile :
- Distortion energy ( 8) σe = √{ [ (240 -0)2 + (0 -(-60))2 + (-60 -240)2 ] /2 } = 275 MPa ; n = 1.27
- Max.shear stress ( 9) σe = 240 - (-60) = 300 MPa ; n = Sy /σe = 1.17
Either theory may be applied to ductiles; the maximum shear stress is clearly more conservative as it predicts a higher equivalent stress.
Brittle :
- Modified Mohr ( 10) 1/n = max( 240/300 , 60/750 , 240/300 -180/750 ) = 0.8 ; n = 1.25
 Copyright 1999-2005 Douglas Wright
Copyright 1999-2005 Douglas Wright
last updated May 2005

 but vanishes at the element in question; its neglect is justified. Other stresses on the element are zero.
but vanishes at the element in question; its neglect is justified. Other stresses on the element are zero.